Introduction
In this project, you will create a Dodecahedron model from recycled materials such as toilet paper or paper towel rolls, and tissue paper boxes for larger models.
Understanding this structure will help us create individual pieces from the paper rolls and see how they connect to form a complete model.
Let’s get started!
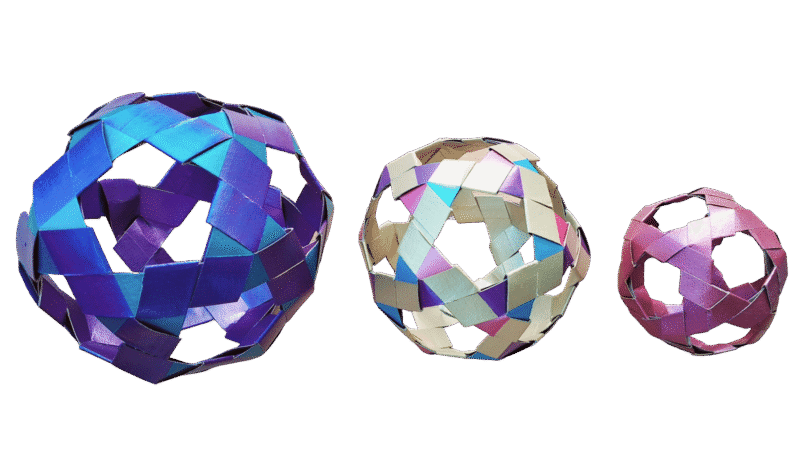
Project Materials

To build a Dodecahedron or Icosidodecahedron model, 30 individual pieces are required per single model. The number of pieces each type of material may produce can vary slightly. This will require a bit of experimentation, but this is the ballpark from our experience:
- 6 Toilet paper rolls
- Each roll typically produces 5–6 individual pieces.
- 2 Paper towel rolls
- Each roll is about three times as long as toilet paper roll and can yield around 18 pieces.
- 3-4 Tissue paper boxes
- Used for larger models.
- Pieces can be cut from either the top (wider) section or side (narrower) panels.
- Each box may produce 8–10 pieces depending on the section used.
Tools and Supplies
- Required
- Protractor, Pencil, and Ruler
- Large Sharp Scissors able to cut thick carton
- Recommended
- Guillotine Paper Cutter for the best experience and straight, sharp edges
- Scoring/Creasing tool or Letter opener (tip of a nail file works great as well, this is optional but we prefer scoring as it does not leave any pencil marks)
- Electric Iron with steamer (very helpful for flattening, plus it takes care of any hygiene concerns regarding working with toilet paper rolls)
- Metallic Acrylic Paint and Paint Brushes
- Masking Tape (required for multi color versions)
- Non-stick parchment paper (if ironing already painted paper rolls to protect the paint and the iron)

Create Individual Units
- Paint Paper rolls first (Optional)
- It’s easier to paint the rolls while they’re still round.
- Allow fully dry before continuing to the next step.
- You may need multiple coats, let each coat fully dry before applying the next coat.
- Flatten the Rolls
- Press each roll flat by hand or use warm iron
- If you’re using an iron, cover the painted roll with a piece of non-stick parchment paper to protect the paint and the iron.
- Measure & Cut
- Place flattened paper roll on your workin surface horisontally
- Using a protractor, mark a 72° angle from the top right corner of the flattened roll, then mark the angled line using pencil or a scoring tool.
- Measure the the angled line and divide it by 5 to calculate the width of individual piece. The width of the piece equials 1/5 of the length, minus a mm or so for some wiggle room.
- Mark the width of the individual peices on the top and bottom edges of the papaer roll and use a pencil or a scoring tool to connect the marks for the rest of the pieces.
- Repeat for all paper rolls until you have marked 30 identical pieces.
- Cut the pieces using scisors or guilliotine paper cutter for clearner look and straight edges.

Assemble the Model
- Start by joining three pieces into a tight triangular interlock to form a vertex.
- Using any open end, interlock 2 more pieces and create a second vertex.
- Keep adding vertices until the pentagon shaped opening is formed, it takes 10 pieces.
- Keep adding pentagon shapes until the model naturally closes up and all 30 pieces are used.
- When finishing off the model you need to detach and re-attach the end of the last piece on the back to close up the model. This is the only step where the glue or clear tape is requred.
- The assembly process is based on priciples of a flat model 1 with the differnce that we are using 72 degree angle cut pieces and making pentagon shaped openings so the structure starts to curve.
Watch the Full Process Video
Next steps
Now that you’ve completed a Dodecahedron model, try your hand at another 3D Model project — the Icosidodecahedron?
This is another 3D model built using our modular-origami–inspired method. It follows the same initial preparation process but introduces a different assembly method similar to Flat Model 2. Give it a try.
Please explore other projects on our website, like drawing your own geometric patterns using a grid — another great way to experience the magic of symmetry and structure.
We’d love to see what you create! Tag @Geomegic on social media to share your work and connect with others in the community.

